Group-NMF with \(\beta\) -divergence

In [1] we propose an approach to speaker identification that relies on group-nonnegative matrix factorisation (NMF) and that is inspired by the I-vector training procedure. Given data measured with several subjects, the key idea in group-NMF is to track inter-subject and intra-subject variations by constraining a set of common bases across subjects in the decomposition dictionaries. This has originally been applied to the analysis of electroencephalograms [2]. The approach presented here extends this idea and proposes to capture inter-class and inter-session variabilities by constraining a set of class-dependent bases across sessions and a set of session-dependent bases across classes. This approach is inspired by the joint factor analysis applied to the speaker identification problem [3]. In the following, first the general NMF framework with \(\beta\) -divergence and multiplicative updates is describe, then we present the group-NMF approach with class and session similarity constraints.

NMF with \(\beta\) -divergence and multiplicative updates

Consider the (nonnegative) matrix \(\textbf{V}\in\mathbb{R}_+^{F\times N}\). The goal of NMF [4] is to find a factorisation for \(\textbf{V}\) of the form:

(1)\[\textbf{V} \approx \textbf{W}\textbf{H}\]

where \(\textbf{W}\in\mathbb{R}_+^{F\times K}\) , \(\textbf{H}\in\mathbb{R}_+^{K\times N}\) and \(K\) is the number of components in the decomposition. The NMF model estimation is usually considered as solving the following optimisation problem:

\[\min_{\textbf{W}\textbf{H}}D(\textbf{V} | \textbf{W}\textbf{H})\quad\mathrm{s.t.}\quad\textbf{W}\geq 0,\ \textbf{H}\geq 0\mathrm{.}\]

Where \(D\) is a separable divergence such as:

\[D(\textbf{V}|\textbf{W}\textbf{H}) = \sum\limits_{f=1}^{F}\sum\limits_{n=1}^{N}d([\textbf{V}]_{fn}|[\textbf{WH}]_{fn})\textrm{,}\]

with \([.]_{fn}\) is the element on column \(n\) and line \(f\) of a matrix and \(d\) is a scalar cost function. A common choice for the cost function is the \(\beta\) -divergence [5] [6] [7] defined as follows:

\[\begin{split}d_{\beta}(x|y)\triangleq \begin{cases} \frac{1}{\beta(\beta -1)} (x^{\beta} + (\beta -1)y^{\beta} - \beta xy^{(\beta-1)})&\beta\in\mathbb{R}\backslash\{0,1\}\nonumber\\ x\log\frac{x}{y} - x + y&\beta=1\nonumber\\ \frac{x}{y} -\log\frac{x}{y} - 1&\beta=0\nonumber\textrm{.} \end{cases}\end{split}\]

Popular cost functions such as the Euclidean distance, the generalised KL divergence [8] and the IS divergence [9] and all particular cases of the \(\beta$-divergence\) (obtained for \(\beta=2\) , \(1\) and \(0\), respectively). The use of the \(\beta\) -divergence for NMF has been studied extensively in Févotte et al. [10]. In most cases NMF problem is solved using a two-block coordinate descent approach. Each of the factors \(\textbf{W}\) and \(\textbf{H}\) is optimised alternatively. The sub-problem in one factor can then be considered as a nonnegative least square problem (NNLS) [11]. The approach implemented here to solve these NNLS problems relies on the multiplicative update rules introduced in Lee et al. [4] for the Euclidean distance and later generalised to the the \(\beta\) -divergence [10] :

(2)\[\textbf{H}\gets \textbf{H}\odot\frac{\textbf{W}^T\left[(\textbf{W}\textbf{H})^{\beta-2}\odot\textbf{V}\right]} {\textbf{W}^T(\textbf{W}\textbf{H})^{\beta-1}}\]

(3)\[\textbf{W}\gets \textbf{W}\odot\frac{\left[(\textbf{W}\textbf{H})^{\beta-2}\odot\textbf{V}\right]\textbf{H}^T } {(\textbf{W}\textbf{H})^{\beta-1}\textbf{H}^T}\mathrm{;}\]

where \(\odot\) is the element-wise product (Hadamard product) and division and power are element-wise. The matrices \(\textbf{H}\) and \(\textbf{W}\) are then updated according to an alternating update scheme.

Group NMF with class and session similarity constraints

In the approach presented above, the matrix factorisation is totally unsupervised and does not account for class variability or session variability. The approach introduced in Serizel et al. [1] intends to take these variabilities into account. It derives from group-NMF [2] and is inspired by exemplar-based approaches for the speaker identification problem [12].

NMF on speaker utterances for speaker identification

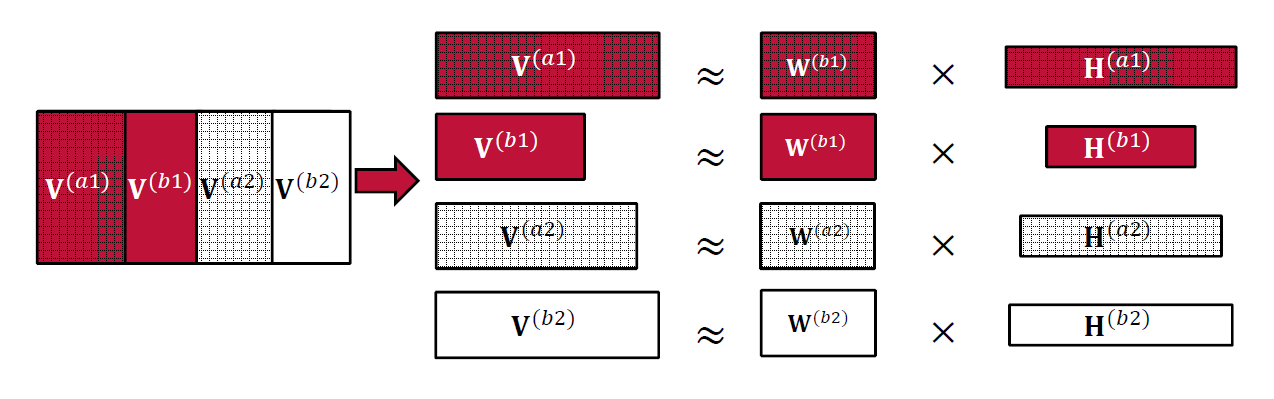
In order to better model speaker identity, we now consider the portion of \(\textbf{V}\) recorded in a session \(s\) in which only the speaker \(c\) is active. This is denoted by \(\textbf{V}^{(cs)}\), its length is \(N^{(cs)}\) and it can be decomposed according to (1):

\[\textbf{V}^{(cs)} \approx \textbf{W}^{(cs)} \textbf{H}^{(cs)}\quad \forall\ (c,s) \in\mathcal{C}\times\mathcal{S}_c\nonumber\]

under nonnegative constraints.

Fig. 1 NMF on speaker utterances

We define a global cost function which is the sum of all local divergences:

(4)\[J_{\mathrm{global}} = \sum\limits_{c = 1}^{C}\sum\limits_{s\in\mathcal{S}_c} D_{KL}(\textbf{V}^{(cs)} | \textbf{W}^{(cs)} \textbf{H}^{(cs)})\mathrm{.}\]

Each \(\textbf{V}^{(cs)}\) can be decomposed independently with standard multiplicative rules ((2), (3)). The bases learnt on the training set are then concatenated to form a global basis. The latter basis is then used to produce features on test sets.

Class and session similarity constraints

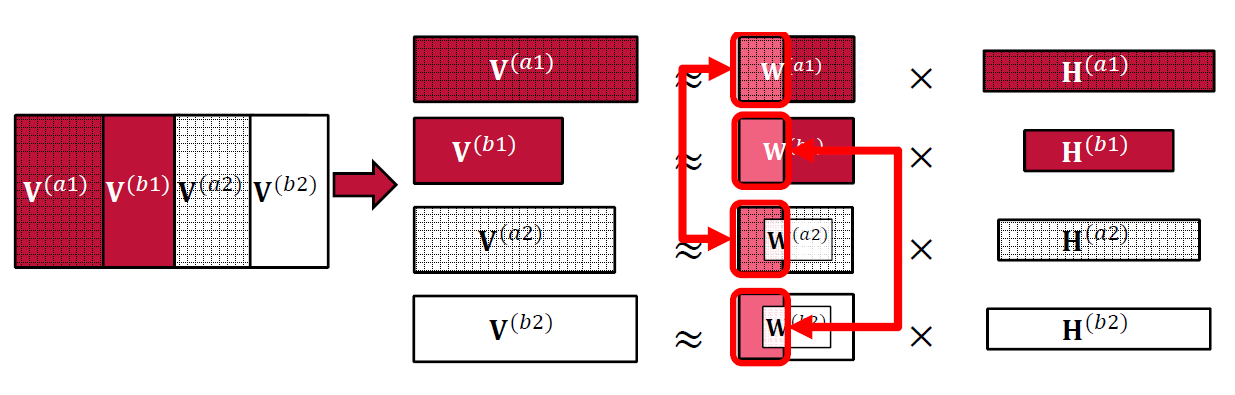
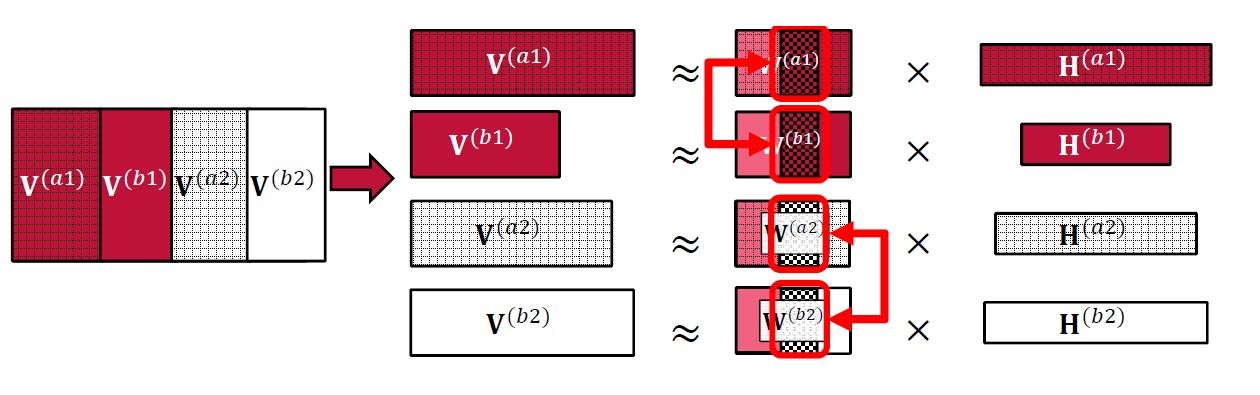
In order to take the session and speaker variabilities into account we propose to further decompose the dictionaries \(\textbf{W}\) similarly as what was proposed by Lee et al. [4]. The matrix \(\textbf{W}^{(cs)}\) can indeed be arbitrarily decomposed as follows:

\[\textbf{W}^{(cs)} = \left[\right.\underset{\leftarrow K_{\mathrm{SPK}}\rightarrow} {\textbf{W}^{(cs)}_{\mathrm{SPK}}}|\underset{\leftarrow K_{\mathrm{SES}}\rightarrow}{\textbf{W}^{(cs)}_{\mathrm{SES}}}|\underset{\leftarrow K_{\mathrm{RES}}\rightarrow}{\textbf{W}^{(cs)}_{\mathrm{RES}}}\left.\right]\]

with \(K_{\mathrm{SPK}} + K_{\mathrm{SES}} + K_{\mathrm{RES}} = K\) and where \(K_{\mathrm{SPK}}\), \(K_{\mathrm{SES}}\) and \(K_{\mathrm{RES}}\) are the number of components in the speaker-dependent bases, the session-dependent bases and the residual bases, respectively.

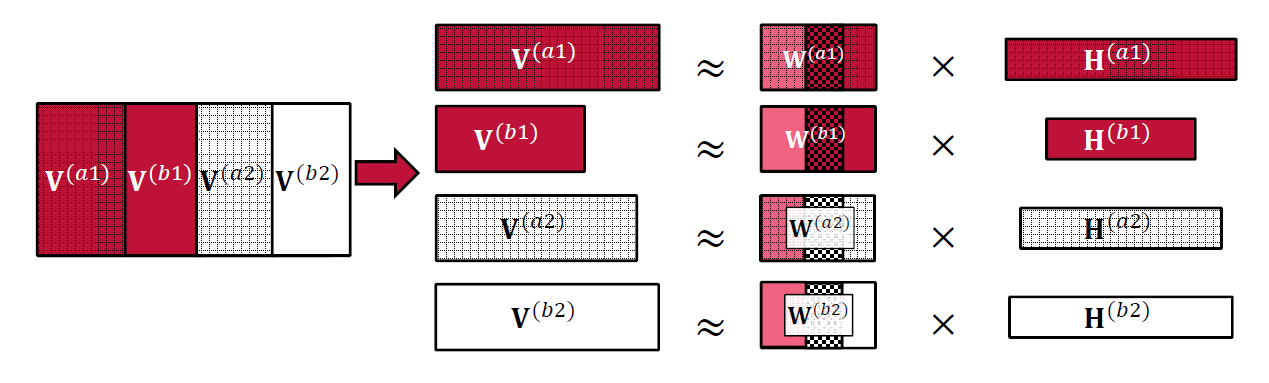
Fig. 2 Basis decomposition into \(\textbf{W}^{(cs)}_{\mathrm{SPK}}\), \(\textbf{W}^{(cs)}_{\mathrm{SES}}\) and \(\textbf{W}^{(cs)}_{\mathrm{RES}}\)

The first target is to capture speaker variability. This is related to finding vectors for the speaker bases (\(\textbf{W}^{(cs)}_{\mathrm{SPK}}\)) for each speaker \(c\) that are as close as possible across all the sessions in which the speaker is present, leading to the constraint:

(5)\[\begin{split}J_{\mathrm{SPK}} = \frac{1}{2}\sum\limits_{c=1}^{C}\sum\limits_{s\in\mathcal{S}_c}\sum\limits_{\substack{s_1\in\mathcal{S}_c \\s_1 \neq s}} \| \textbf{W}^{(cs)}_{\mathrm{SPK}} - \textbf{W}^{(cs_1)}_{\mathrm{SPK}}\|^2 < \alpha_1\end{split}\]

with \(\|.\|^2\) the Euclidean distance and \(\alpha_1\) is the similarity constraint on speaker-dependent bases.

Fig. 3 Speaker similarity constraint

The second target is to capture session variability. This can be accounted for by finding vectors for the sessions bases (\(\textbf{W}^{(cs)}_{\mathrm{SES}}\)) for each session \(s\) that are as close as possible across all the speakers that speak in the session, leading to the constraint:

(6)\[\begin{split}J_{\mathrm{SES}} = \frac{1}{2}\sum\limits_{s=1}^{S}\sum\limits_{c\in\mathcal{C}_s}\sum\limits_{\substack{c_1\in\mathcal{C}_s \\c_1 \neq c}} \| \textbf{W}^{(cs)}_{\mathrm{SES}} - \textbf{W}^{(c_1s)}_{\mathrm{SES}}\|^2 < \alpha_2\end{split}\]

where \(\alpha_2\) is the similarity constraint on session-dependent bases.

Fig. 3 Session similarity constraint

The vectors composing the residual bases \(\textbf{W}^{(cs)}_{\mathrm{RES}}\) are left unconstrained to represent characteristics that depend neither on the speaker nor on the session.

Minimizing the global divergence (4) subject to constraints (5) and (6) is equivalent to the following problem:

(7)\[\min\limits_{\textbf{W},\textbf{H}} J_{\mathrm{global}} + \lambda_1 J_{\mathrm{SPK}} + \lambda_2 J_{\mathrm{SES}}\quad\mathrm{s.t.} \quad\textbf{W}\geq 0,\ \textbf{H}\geq 0\]

which in turn leads to the multiplicative update rules for the dictionaries \(\textbf{W}^{(cs)}_{\mathrm{SPK}}\) and \(\textbf{W}^{(cs)}_{\mathrm{SES}}\):

\[\begin{split}\textbf{W}_{\mathrm{SPK}}^{(cs)}&\leftarrow \textbf{W}_{\mathrm{SPK}}^{(cs)}\odot\frac{\left[(\textbf{W}^{(cs)}\textbf{H}^{(cs)})^{-1}\odot\textbf{V}^{(cs)}\right]{\textbf{H}_{\mathrm{SPK}}^{(cs)}}^T + \frac{\lambda_1}{2}\sum\limits_{\substack{s_1\in\mathcal{S}_c\\s_1\neq s}}\textbf{W}_{\mathrm{SPK}}^{(cs_1)}} {\textbf{1}{\textbf{H}_{\mathrm{SPK}}^{(cs)}}^T + \frac{\lambda_1}{2} \left(\mathrm{Card}(\mathcal{S}_c) - 1\right)\textbf{W}_{\mathrm{SPK}}^{(cs)}}\\ \textbf{W}_{\mathrm{SES}}^{(cs)}&\leftarrow \textbf{W}_{\mathrm{SES}}^{(cs)}\odot\frac{\left[(\textbf{W}^{(cs)}\textbf{H}^{(cs)})^{-1}\odot\textbf{V}^{(cs)}\right]{\textbf{H}_{\mathrm{SES}}^{(cs)}}^T + \frac{\lambda_2}{2}\sum\limits_{\substack{c_1\in\mathcal{C}_s\\c_1\neq c}}\textbf{W}_{\mathrm{SES}}^{(c_1s)}} {\textbf{1}{\textbf{H}_{\mathrm{SES}}^{(cs)}}^T + \frac{\lambda_2}{2} \left(\mathrm{Card}(\mathcal{C}_s) - 1\right)\textbf{W}_{\mathrm{SES}}^{(cs)}}\end{split}\]

We obtained these update rules using the well know heuristic which consists in expressing the gradient of the cost function (7) as the difference between a positive contribution and a negative contribution. The multiplicative update then has the form of a quotient of the negative contribution by the positive contribution. The update rules for \(\textbf{W}^{(cs)}_{\mathrm{RES}}\) are similar to the standard rules:

\[\textbf{W}_{\mathrm{RES}}^{(cs)}\leftarrow \textbf{W}_{\mathrm{RES}}^{(cs)}\odot\frac{\left[(\textbf{W}^{(cs)}\textbf{H}^{(cs)})^{-1}\odot\textbf{V}^{(cs)}\right]{\textbf{H}_{\mathrm{RES}}^{(cs)}}^T }{\textbf{1}{\textbf{H}_{\mathrm{RES}}^{(cs)}}^T}\mathrm{.}\nonumber\]

Note that the update rules for the activations (\(\textbf{H}^{(cs)}\)) are left unchanged.

Download

Source code available at https://github.com/rserizel/groupNMF

Citation

If you are using this source code please consider citing the following paper:

Reference

18. Serizel, S. Essid, and G. Richard (2016, March). “Group nonnegative matrix factorisation with speaker and session variability compensation for speaker identification”. In Proc. of ICASSP, pp. 5470-5474, 2016.

Bibtex

@inproceedings{serizel2016group,

title={Group nonnegative matrix factorisation with speaker and session variability compensation for speaker identification},

author={Serizel, Romain and Essid, Slim and Richard, Ga{“e}l},

booktitle={2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP)},

pages={5470–5474},

year={2016},

organization={IEEE} }

References

[1]	Serizel, S. Essid, and G. Richard, “Group nonnegative matrix factorisation with speaker and session variability compensation for speaker identification”. In Proc. of ICASSP, pp. 5470-5474, 2016.

[2]	Lee and S. Choi, “Group nonnegative matrix factorization for EEG classification,” in Proc. of AISTATS, pp. 320–327, 2009.

[3]	Kenny, G. Boulianne, P. Ouellet, and P. Dumouchel, “Joint factor analysis versus eigenchannels in speaker recognition,” IEEE Transactions on Audio, Speech and Language Processing, vol. 15, pp. 1435–1447, 2007.

[4]	Lee and H. S. Seung, “Learning the parts of objects by non-negative matrix factorization.,” Nature, vol. 401, no. 6755, pp. 788–791, 1999.

[5]	Basu, I. R. Harris, N. L. Hjort, and M. C. Jones, “Robust and efficient estimation by minimising a density power divergence,” Biometrika, vol. 85, no. 3, pp. 549–559, 1998.

[6]	Cichocki and S. Amari, “Families of alpha-beta-and gamma-divergences: Flexible and robust measures of similarities,” Entropy, vol. 12, no. 6, pp. 1532–1568, 2010.

[7]	Eguchi and Y. Kano, “Robustifing maximum likelihood estimation,” Research Memo 802, Institute of Statistical Mathematics, June 2001.

[8]	Kullback and R. A. Leibler, “On information and sufficiency,” The annals of mathematical statistics, pp. 79–86, 1951.

[9]	Itakura, “Minimum prediction residual principle applied to speech recognition,” IEEE Transactions on Acoustics, Speech and Signal Processing, vol. 23, no. 1, pp. 67–72, 1975.

[10]	Févotte and J. Idier, “Algorithms for nonnegative matrix factorization with the beta-divergence,” Neural Computation, vol. 23, no. 9, pp. 2421–2456, 2011.

[11]	Gillis, “The why and how of nonnegative matrix factorization,” in Regularization, Optimization, Kernels, and Support Vector Machines, M. Signoretto J.A.K. Suykens and A. Argyriou, Eds., Machine Learning and Pattern Recognition Series, pp. 257 – 291. Chapman & Hall/CRC, 2014.

[12]	Hurmalainen, R. Saeidi, and T. Virtanen, “Noise Robust Speaker Recognition with Convolutive Sparse Coding,” in Proc. of Interspeech, 2015.